Агрегирующие функции, меры и формулы
Неотъемлемой частью OLAP-модели является задание функций агрегирования. Поскольку целью OLAP является создание многоуровневой модели анализа, данные на уровнях, отличных от фактического, должны быть соответствующим образом агрегированы. Важно отметить, что по каждому измерению можно задавать собственную (и не одну) функцию агрегации. Таким образом, в случае куба с

измерениями функция агрегирования:
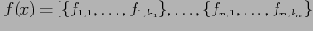
где

— точка куба, а

-

-ая функция агрегирования по

-ому измерению.
В [7] приведена следующая классификация агрегирующих функций с точки зрения сложности распараллеливания.
Категории агрегирующих функций
Дистрибутивные функции
позволяют разбивать входные данные и вычислять отдельные итоги, которые потом можно объединять.
Алгебраические функции
можно представить комбинацией из дистрибутивных функций (например, Average() можно представить как
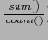
Холистические функции
невозможно вычислять на частичных данных или представлять каким-либо образом.
Эта классификация окажется полезной, когда мы будем рассматривать классы разбиения в алгоритме Quotient Cube (см. раздел , работы [12],[11],[26]), в котором разбиение по покрытию применимо для дистрибутивных и алгебраических функций.
Вперед: Виды запросов к кубам
Выше: Введение. Анализ задачи
Назад: История Задачи