Доказательство
Авторы опускают необходимую при создании DWARF-куба лексикографическую сортировку начальной таблицы (во время создания куба появление нового префикса означает необходимость создания новой вершины на уровне, где различаются префиксы). Сортировка всей фактической таблицы —
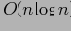
или

в лучшем случае (сортировка слиянием, кучами или подсчетом, вычерпыванием). Но с учетом NP-полноты начальной задачи, этим затратами можно пренебречь.
Пусть существует таблица фактических данных с

измерениями (
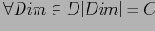
), и количество фактических кортежей
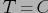
. Не нарушая общности, положим
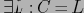
. У получившегося сжатого куба (или DWARF-куба) корневая ячейка будет иметь вид, показанный на рисунке . Группа

содержит ячейки, не имеющие связи с фактическими кортежами, группа

— ячейки, связанные с одним кортежем фактической таблицы,

— два фактических кортежа.
Вершина G, разбитая на группы, где группа

связана с

фактическими кортежами
Лемма 1
Если из набора равномерно распределенных

элементов выбрать некоторый элемент и повторить выбор

раз, то вероятность выбора этого элемента ровно

раз приблизительно равна:
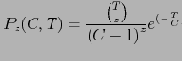
Равномерность — еще одно ограничение на входные фактические данные. В общем случае:
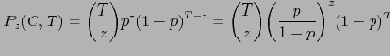
Коротко укажем дальнейшие пункты доказательства.
Применяя лемму 1 к группам

и подставляя
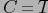
Лемма 2
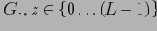
содержит
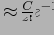
ячеек, которые адресуют ровно

кортежей.
В общем случае в

попадает
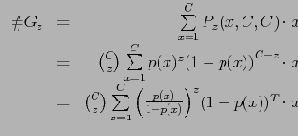
В случае неравномерного распределения кортежей, данная сумма будет отличаться от результатов [22], и это повлечет изменение всех дальнейших оценок в леммах.
Лемма 3
Число дубликатных ключей в вершине, на которую указывает ячейка группы

равно 0. (
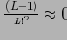
)
Основываясь на введенных выше понятиях левого и хвостового сжатий, можно показать, что
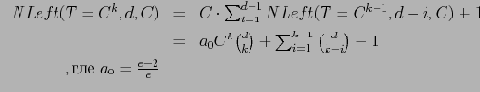
и
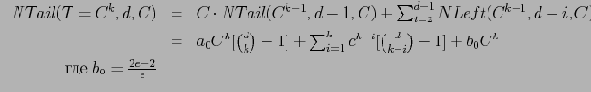
Здесь

— число ячеек, подвергающихся левому сжатию, и

— число ячеек, подвергающихся хвостовому сжатию.
Из последней формулы получим следующее соотношение для числа ячеек куба:
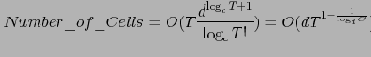
А поскольку при устранении суффиксной избыточности DWARF, в отличие от других алгоритмов, проверяет каждую ячейку только один раз (автору неизвестны алгоритмы, которые для устранения суффиксной избыточности не проверяли бы каждую ячейку экспоненциальное число раз), получаем ту же оценку и для сложности работы алгоритма.