Пример Вычислений
Рассмотрим в качестве примера трехмерный массив данных, состоящий из измерений A, B и С. Он разбит на небольшие блоки, помещающиеся в оперативной памяти. Допустим, всего получилось 64 блока. Измерение А разбито на четыре равномерных участка,
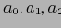
и

. Измерения B и С также разбиты на 4 участка каждое. Блоки 1, 2,..., 64 относятся к подкубам
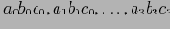
соответственно. Предположим, что размерность измерений A, B и С составляет 40, 400 и 4000 соответственно. Тогда размеры массивов для измерений составляют 40, 400 и 4000 соответственно. Размеры участков, на которые разбиты измерения, составляют 10, 100 и 1000. Полная материализация куба предполагает вычисление всех подкубов, составляющих этот куб. В результате полный куб состоит из следующих подкубов:
Рассмотрим, каким образом используется MultiWay в таком случае. Существует множество вариантов порядка, в котором подкубы копируются в оперативную память для вычислений. Подкубы пронумерованы в порядке, указанном на рис. . Предположим, мы хотим вычислить блок

подкуба BC. Под этот блок выделяется память в специальном участке памяти, выделенном для создания куба. Для вычисления этого блока требуется использовать блоки с 1-го по 4-ый подкуба ABC. Таким образом, ячейки для

вычисляются агрегированием по A (
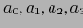
). После этого память может быть использована для построения следующего блока

, который вычисляется агрегированием следующих 4 блоков ABC: с 5-го по 8-ой. Продолжая таким образом, мы можем вычислить весь подкуб BC.
Следовательно, в основной памяти достаточно располагать только один блок BC, и эта память используется для вычисления всех блоков подкуба BC.
 |
В процессе вычисления подкуба BC мы были вынуждены прочитать все 64 блока. Однако в большинстве случаев существует возможность избежать повторного чтения этих блоков при вычислении прочих подкубов (таких как AC и AB). Для решения этой задачи и используются многопозиционное агрегирование и одновременное вычисление нескольких кубов. К примеру, при сканировании блока 1 (

) для вычисления двухмерного блока

, могут быть вычислены все остальные двухмерные блоки, относящиеся к

. Во время пребывания

в оперативной памяти вычисляются блоки

,

и

по всем двухмерным подкубам. Таким образом, пока трехмерный блок находится в памяти, MultiWay одновременно агрегирует все соответствующие двухмерные блоки.
Порядок, в котором читаются блоки и вычисляются подкубы, определяет общую эффективность вычислений. Рассмотрим тот же пример с учетом размерностей измерений (40, 400, 4000 для А, В и С соответственно). Тогда наибольшим двухмерным кубом является BC, его размер
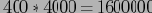
. Следующий по размеру подкуб AC, его размер
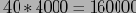
. AB — наименьший двухмерный куб размером
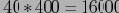
Предположим, что блоки читаются в указанном порядке, от 1 к 64. При таком порядке наибольший двухмерный куб BC полностью вычисляется для каждого кортежа. Т.е.

полностью агрегируется на основе участка, содержащего блоки 1-4;

полностью вычисляется на основе участка, содержащего блоки 5-8 и так далее. Для сравнения, полное вычисление одного блока второго по размеру двухмерного подкуба АС в том же порядке 1-64 требует просмотра 13 блоков. К примеру,

агрегируются после просмотра блоков 1, 5, 9 и 13. Наконец, для вычисление последнего двухмерного подкуба АВ потребуется 49 блоков.

полностью вычисляются после просмотра блоков 1, 17, 33 и 49. Таким образом, для вычисления АВ требуется самый длительный просмотр блоков.
Чтобы избежать загрузки трехмерного блока в оперативную память несколько раз, требуется оперативнвя память следующего объема:
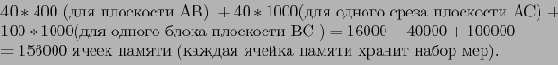
Предположим что блоки считываются в порядке 1, 17, 33, 49, 5, 21, 27, 53 и так далее. Тогда сначала вычисляется плоскость AB, затем АС и в конце ВС. Минимальный размер памяти, необходимой для двухмерных блоков, в таком случае составит:
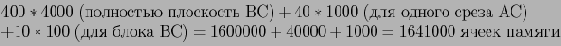
На порядок больше, чем в предыдущем примере.
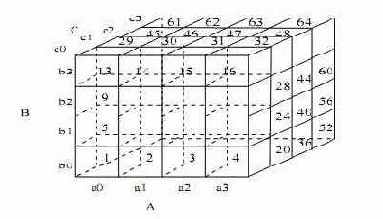
Аналогично можно вычислить минимальные требования к памяти для вычисления одномерных и нульмерных подкубов. На рисунке изображены наиболее и наименее эффективные пути вычисления. Самое эффективный порядок просмотра: 1-64.
Рис. 2.6:
Различные пути построения подкубов в MultiWay
В приведенном примере предполагается, что имеется достаточно памяти для однопроходного вычисления куба (вычисления всех подкубов за одно чтение всех блоков). Если памяти недостаточно, то может понадобится несколько чтений трехмерного массива. Но и в таких случаях общий подход выбора оптимального порядка чтения блоков остается неизменным. MultiWay наиболее эффективен, когда размерности измерений относительно небольшие и данные не слишком разрежены. Когда размерность измерений очень велика или данные сильно разрежены, массивы становятся слишком большими для загрузки в оперативную память, и метод теряет эффективность.
Экспериментально показано, что при соответствующем выборе техники обработки разреженных массивов и тщательном упорядочивании подкубов MultiWay намного эффективней традиционных ROLAP-вычислений. В отличие от ROLAP, MultiWay не требует дополнительного места для хранения индексов. Более того, в MultiWay используется прямая адресация в массивах, что намного быстрее чтения по ключу в ROLAP-методах. Для ROLAP-вычислений куба было бы эффективней сначала развернуть куб в памяти в многомерный массив, пересчитать и записать результаты в таблицу. Однако подобный подход эффективен при небольшой размерности кубов, ведь количество подкубов растет экспоненциально при добавлении измерений.
MultiWay неэффективен для вычисления кубов типа айсберг, поскольку невозможно использовать . Вычисления в MultiWay идут "снизу-вверх", поэтому нельзя отбросить ни одну из веток вычислений, т.к. сначала просматриваются детальные ячейки, и даже если они не удовлетворяют заданному условию, возможно, этому условию уже удовлетворяют агрегированные ячейки.
Вперед: Аппроксимирующие алгоритмы
Выше: Синтаксические алгоритмы
Назад: Алгоритм Dwarf