QC-Trees
QC-Tree — дерево с разделением префиксов, где грани представляются строчками, а связи отражают необходимые отношения drill-down. Основной идеей QC-деревьев является то, что верхние грани классов куба хранят всю необходимую информацию для выполнения запросов. Т.е. при данном подходе не хранятся даже нижние грани классов. При такой структуре хранения данных запросы над Quotient-кубами выполняются эффективнее запросов над DWARF-кубами. Достигается это превосходство на основе аналогичного по смыслу устранения суффиксной и префиксной избыточностей. QC-деревья позволяют устранять суффиксную избыточность за счет того, что хранятся только классы, а не отдельные ячейки. Префиксная избыточность устраняется за счет свойств самой структуры QC-tree.
Определение 5.5 QC-Tree куба Q — это орграф
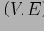
, в котором:
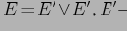
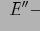
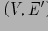
— это дерево;

существует и единственна вершина
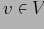
такая, что строчное представление

совпадает с последовательностью меток вершин на пути от корня к

в (V,

); эта вершина хранит агрегирующее значение для

.

и

— классы в

,
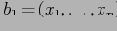
и
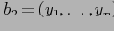
— их верхние грани, и что


(например, что

напрямую специализирует (drills-down)

) в

; тогда для каждого измерения

, на котором различаются

и

, существует либо ребро дерева, либо связь (маркированная

) из вершины
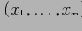
в вершину
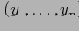
.
Только последнее из условий требует каких-либо объяснений. Оно просто утверждает, что если С напрямую специализирует D в Q, то это возможно либо по ребру дерева, либо по связи из какого-либо префикса пути, представляющего верхнюю грань С, к вершине, которая приведет к верхней грани D.
| Класс | Верхняя Грань |
| С1 | (ALL,ALL,ALL) |
| С2 | (R1,ALL,ALL) |
| С3 | (ALL,книги,ALL) |
| С4 | (ALL,ALL,осень) |
| С5 | (R1,книги,весна) |
| С6 | (R1,еда,осень) |
| С7 | (R2,книги,осень) |
QC-Tree
Доказана теорема, о том, что QC-дерево для каждого Quotient куба уникально. Существуют алгоритмы создания/поддержки QC-деревьев. Выполнение запросов на QC-деревьях сильно отличается от аналогичных алгоритмов в других методах, т.к. необходимо ''выводить'' содержимое ячейки из верхней и нижней гранях класса. Аналогично, поддержка изменений информации требует пересмотра решетки классов, что, в общем случае, замедляет внесение изменений. В таблице показаны классы и верхние грани Quotient-куба для примерных данных из таблицы , а на рис. — соответствующее QC-Tree.