Сложность

Несмотря на то, что показана NP-полнота общей задачи выбора представлений для материализации [10], в работе [22] были даны новые оценки сложности алгоритма DWARF. Большая часть этих результатов вошла в данный раздел. При этом хотелось бы в очередной раз подчеркнуть, что DWARF — алгоритм полной материализации (materialize-all). Также хотелось бы отметить, что оценки в работе [22] были получены при наложении определенных условий на начальные данные.

С помощью приведенной ниже модели можно показать, что вычислительная сложность алгоритма и объем результирующего куба равны:

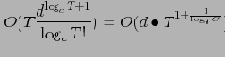
— число измерений

— мощность измерения

— число фактических кортежей

Приведем некие трактовки данного результата.

Положим, размерность куба растет , т.е. все кортежи фактической таблицы ''расширяются'' путем добавления новых столбцов. Тогда:

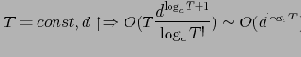
Причем

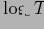
для реальных баз данных довольно мало.

Правая часть равенства показывает, что размер и время вычисления куба при постоянном числе измерений и добавлении новых фактических кортежей растет почти полиномиально от T, которое возводится в

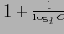
(что очень близко к единице для больших фактических таблиц).

Модель опирается на понятия префиксной, суффиксной избыточности, приведенные выше в описании алгоритма (см. ). Разобьем категории сжатия на две группы:

сжатие связанности (implication coalescing)

Содержание раздела

---

---