Точечные запросы
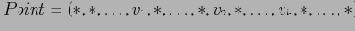
, где если
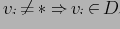

.
Алгоритм.
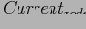
= корень;
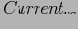
=

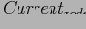
искать дугу с меткой
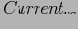
,
если существует:
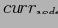
= потомок по найденной дуге;
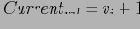
иначе: проверить последнее измерение j, по которому у
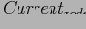
есть потомок.
Если
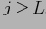
, тогда

в кубе не появится.
Иначе:
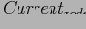
= потомок по измерению j, снова повторяем 2.
Примеры

начинаем с корня, находим вершину 7, в вершине 7 ищем ''осень'', берем потомка по измерению, продукты, попадаем в 9 — есть ответ.

все тоже самое, но в 9 мы будем пытаться найти ''весна''

такой ячейки нет

(*,еда,*)

в 5, но там нет значения, ''проваливаемся'' в 6 — ответ