Обзор алгоритмов MOLAP
       

Вейвлеты


Одной из самых успешных (с точки зрения ожидаемых результатов) работ в области аппроксимации OLAP-данных является [24].

Основными посылками работы явились два наблюдения:

  • часто встречаются ситуации, когда пользователь предпочтет не точный результат, а некоторый приближенный, особенно если последний можно получить на порядок быстрее;

  • для ряда приложений возможны ситуации, когда недоступен источник данных, а существует необходимость обработать запрос, даже получив не совсем точный результат.

    Рассмотрим особенности работы этого алгоритма. Прежде всего отметим, что это алгоритм нацелен на оптимизацию только одного типа запросов — (range-sum query).

    Range-sum query:

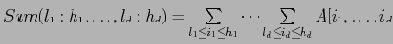
    Шаги алгоритма:

    Шаг Первый

    Формируется куб частичных сумм (partial sum cube) — куб, в котором ячейки представляют собой многомерные суммы всех прилежащих ячеек. Это представление данных хорошо тем, что ячейки куба частичных сумм монотонно не убывают по всем измерениям, поэтому аппроксимация подобного куба является более точной, нежели аппроксимация исходного куба. Для ответа на интервальный запрос требуется оценка значения лишь в одной ячейке, а не в целом наборе ячеек.

    Partial Sum Cube:

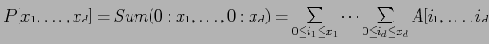
    Шаг Второй

    Создается новый куб, в котором каждая в каждой ячейке содержится натуральный логарифм значения соответствующей ячейки из куба частичных сумм. Таким образом, еще больше ''сглаживаются'' колебания значений.

    Шаг Третий

    Формируется декомпозиция получившегося куба, основанная на вейвлетах ( в простейшем случае, хоаровских вейвлетах), — декомпозиция неоднократно применяется для каждого из измерений; таким образом, куб ''складывается'' по каждому из измерений.

    Пример декомпозиции сигнала

    Положим, у нас есть одномерный набор значений

    .

    Таблица 3.1:

    Декомпозиция сигнала вейвлетами

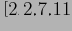
    Конечное преобразование сигнала будет выглядеть так

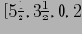
    . Подобные преобразования могут выполняться очень быстро. Детальные коэффициенты в данном примере нормализуются по уровню.

    В ходе таких преобразований информация не теряется и не приобретается.
    Подобная декомпозиция больших объемов данных показывает, что часто коэффициенты, начиная с некоторого значения, отличаются очень слабо. Поэтому мы можем усреднять коэффициенты, считая, что подобные преобразования не сильно повлияют на конечный результат.

    Шаг Четвертый

    На следующем этапе мы выбираем



    главных коэффициентов вейвлетовой декомпозиции данных. Остальные


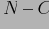
    коэффициентов мы получаем, усредняя начальные


    коэффициентов. Хранятся только


    коэффициентов куба.

    Таким образом, можно сильно сократить объем хранимых данных, почти не теряя в точности результата. Скорость обработки запросов растет в соответствии с уменьшением объема хранимых данных и возможностью обработки запросов путем обращения только к одной ячейке и последующих преобразований данных. При соответствующем выборе коэффициентов скорость этого алгоритма при обработке интервальных запросов превосходит скорость всех других существующих алгоритмов при малом значении ошибки данных.

    К сожалению, несмотря на всю эффективность этого метода, он подходит лишь для обработки только одного типа запросов. Более того, для создания кубов этот алгоритм требует достаточного объема вычислений, и результирующий куб почти невозможно изменять при изменениях данных. Применение этого алгоритма ограничено также и тем, что необходимо тщательно выбирать коэффициент


    , основываясь на заданном допустимом значении ошибки.

    Вперед: Вычисление Iceberg кубов

    Выше: Аппроксимирующие алгоритмы

    Назад: Аппроксимирующие алгоритмы

     


    Содержание раздела