Оптимизация сортировки больших массивов данных
"По оценкам производителей компьютеров в 60-х годах в среднем более четверти машинного времени тратилось на сортировку. Во многих вычислительных системах на нее уходит больше половины машинного времени…" Дональд Э. Кнут "Искусство программирования. Том 3. Сортировка и поиск".
…прошло полвека. Процессорные мощности за это время необычайно возросли, но ситуация с сортировкой навряд ли значительно улучшилось. Так, на AMD Athlon 1050 MHz упорядочивание миллиона чисел одним из лучших алгоритмов сортировки – quick sort – занимает 3,6 сек., а десяти миллионов – уже свыше пяти минут (см. рис. graph 33). Сортировка сотен миллионов чисел вообще требует астрономических количеств времени. И это при том, что сортировка – она из наиболее распространенных операций, встречающееся буквально повсюду. Конечно, потребность в сортировке сотен миллионов чисел есть разве что у ученых, моделирующих движения звезд в галактиках или расшифровывающих геном, но ведь и в бизнес приложениях таблицы данных с сотнями тысяч записей – не редкость! Причем, к производительности интерактивных приложений предъявляются весьма жесткие требования, – крайне желательно, чтобы обновление ячеек таблицы происходило параллельно с работой пользователя, т.е. осуществлялась налету.
Алгоритму быстрой сортировки требуется O(n lg n) операций в среднем и O(n2) в худшем случае. Это действительно очень быстрый алгоритм, который навряд ли можно значительно улучшить. Действительно, нельзя. Но надо! Вспомните Понедельник Стругакцих: "Мы сами знаем, что она [задача] не имеет решения, - сказал Хунта, немедленно ощетинившись. – Мы хотим знать, как ее решать"
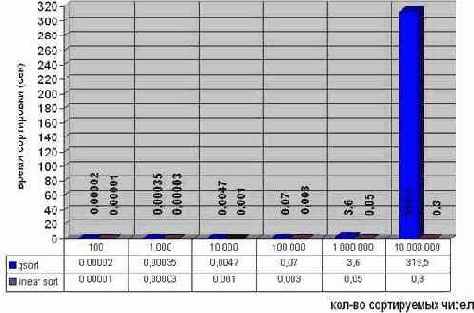
Рисунок 55 graph 0x33 Время сортировки различного количества чисел алгоритмами quick sort и linear sort
Ведь существует же весьма простой и эффективный алгоритм сортировки, требующий в худшем случае порядка O(n) операций. Нет, это не шутка и не первоапрельский розыгрыш! Такой алгоритм действительно есть.
Так, на компьютере AMD Athlon 1050 он упорядочивает десять миллионов чисел всего 0,3 сек, что в тысячу раз быстрее quick sort!
Впервые с этим алгоритмом мне пришлось столкнуться на олимпиаде по информатике, предлагающей в одной из задач отсортировать семь чисел, используя не более трех сравнений. Решив, что по такому поводу не грех малость повыпендриваться, я быстро написал программку, которая выполняла сортировку, не используя вообще ни одного сравнения. К сожалению, по непонятным для меня причинам, решение зачтено не было, и только спустя пару лет, изучив существующие алгоритмы сортировки, я смог оценить не тривиальность полученного результата.
Собственно, вся идея заключалась в том, что раз неравенство k + 1 > k > k – 1 справедливо для любых k, то можно сопоставить каждому числу kx соответствующую ему точку координатной прямой и в итоге мы получим… "естественным образом" отсортированную последовательность точек. Непонятно? Давайте разберем это на конкретном примере. Пусть у нас имеются числа 9, 6, 3 и 7. Берем первое из них – 9 – отступаем вправо на девять условных единиц от начала координатной прямой и делам в этом месте зарубку. Затем берем следующее число – 6– и повторяем с ним ту же самую операцию… В конечном счете у нас должно получится приблизительно следующее (см. рис. 44).
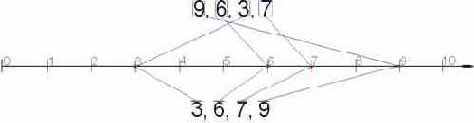
Рисунок 56 0х44 Сортировка методом отображения
А теперь давайте, двигаясь по координатной прямой слева направо просто выкинем все неотмеченные точки (или, иначе говоря, выделим отмеченные). У нас получится… получиться последовательность чисел, упорядоченная по возрастанию! Соответственно, если двигаться по прямой справа налево, мы упорядочим числа по убыванию.
И вот тут мы подходим к самому интересному! Независимо от расположения сортируемых чисел, количество операций, необходимых для их упорядочивания, всегда равно: N+VAL_N, где N – количество сортируемых чисел, а VAL_N – наибольшее количество значений, которые могут принимать эти числа.
Поскольку, VAL_N константа, из формулы оценки сложности алгоритма ее можно исключить и тогда она (формула сложности) будет выглядеть так: O(N). Wow! У вам уже чешутся руки создать свою первую реализую? Что ж, это нетрудно. Заменим числовую ось одномерным массивом и вперед:
#define DOT 1
#define NODOT 0
int a;
int src[N];
int coordinate_line[VAL_N];
memset(coordinate_line, NODOT, VAL_N*sizeof(int));
// ставим на прямой зарубки в нужных местах
for (a = 0; a < N; a++)
coordinate_line[src[a]]=DOT;
// просматриваем прямую справа налево в поисках зарубок
// все "зарубленные" точки копируем в исходный массив
for(a = 0; a < N_VAL; a++)
if (coordinate_line[a]) { *src = a; src++;}
Листинг 44 Простейший вариант реализации алгоритма линейной сортировки
Ага! Вы уже заметили один недостаток этой реализации алгоритма? Действительно, побочным эффектом такой сортировки становится отсечение всех "дублей", т.е. совпадающих чисел. Возьмем, например, такую последовательность: 3, 9, 6, 6, 3, 2, 9. После сортировки мы получим: 2, 3, 6, 9. Знаете, а с одной стороны это очень даже хорошо! Ведь зачастую "дубли" совершенно не нужны и только снижают своим хламом производительность.
Хорошо, а как быть если уничтожение дублей в таком-то конкретном случае окажется неприемлемо? Нет ничего проще, – достаточно лишь слегка модифицировать наш алгоритм, не просто ставя зарубку на координатной прямой, но еще и подсчитывая их количество в соответствующей ячейке массива. Усовершенствованный вариант реализации может выглядеть, например, так:
int* linear_sort(int *p, int n)
{
int N;
int a, b;
int count = 0;
int *coordinate_line; // массив для сортировки
// выделяем память
coordinate_line = malloc(VAL_MAX*sizeof(int));
if (!coordinate_line) /* недостаточно памяти */
return 0;
// init
memset(coordinate_line, 0, VAL_MAX*sizeof(int));
// сортировка
for(a = 0; a < n; a++)
coordinate_line[p[a]]++;
// формирование ответа
for(a = 0; a < VAL_MAX; a++)
for(b = 0; b < coordinate_line[a]; b++)
p[count++]=a;
// освобрждаем память
free(coordinate_line);
return p;
}
Листинг 45 [Memory/sort.linear.c] Пример улучшенной реализации алгоритма линейной сортировки
Давайте сравним его с quick sort при различных значениях N и посмотрим насколько он окажется эффективен. Эксперименты, проведенные автором, показали, что даже такая примитивная реализация линейной сортировки намного превосходит quick sort и при малом, и при большом количестве сортируемых значений (см. рис. graph 32). Причем, этот результат можно существенно улучшить если прибегнуть к услугам разряженных массивов, а не тупо сканировать virtual_array целиком!
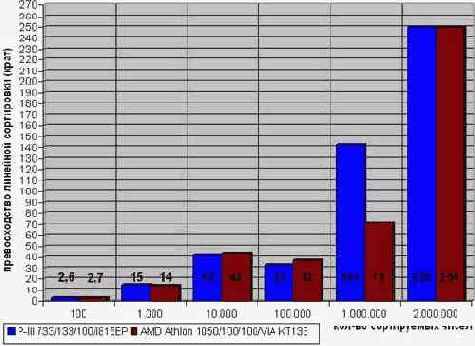
Рисунок 57 graph 32 Превосходство линейной сортировки над qsort. Смотрите, линейная сортировка двух миллионов чисел (вполне реальное количество, правда) выполняется в двести пятьдесят раз быстрее!
Но не все же время говорить о хорошем! Давайте поговорим и о печальном. Увы, за быстродействие в данном случае приходится платить оперативной памятью. Алгоритм линейной сортировки пожирает ее прямо-таки в чудовищных количествах. Вот приблизительные оценки.
Очевидно, количество ячеек массива coordinate_line
равно количеству значений, которые могут принимать сортируемые данные. Для восьми битных типов char это составляет 28=256 ячеек, для шестнадцати и тридцати двух битных int – 216= 65.536 и 232= 4.294.967.296 соответственно. С другой стороны, каждая ячейка массива coordinate_line
должна вмещать в себя максимально возможное количество дублей, что в худшем случае составляет N. Т.е. в большинстве ситуаций под нее следует отводить не менее 16, а лучше все 32 бита. Учитывая это, составляем следующую нехитрую табличку.
|
тип данных |
кол-во требуемой памяти при сохранении дублей |
кол-во требуемой памяти без сохранения дублей |
|
char |
1 Кб |
32 байта |
|
char (без учета знака) |
512 байт |
16 байт |
|
_int16 |
256 Кб |
8 Кб |
|
_int16 (без учета знака) |
128 Кб |
4 Кб |
|
_int32 |
16 Гб |
1 Гб |
|
_int32 (без учета знака) |
8 Гб |
256 Кб |
Таблица 5 Количество памяти, потребляемой алгоритмом линейной сортировки при упорядочивании данных различного типа
Ничегошеньки себе потребности! Для сортировки 32-разядных элементов с сохранением "дублей" потребуется восемь гигабайт оперативной памяти! Конечно, 99.999% ячеек памяти будут пустовать и потому подкачка страниц с диска не сильно ухудшит производительность, но… Вся проблема как раз и заключается в том, что нам просто не дадут этих восьми гигабайт. Операционные системы Windows 9x/NT ограничивают адресное пространство процессора всего четырьмя гигабайтами, причем больше двух из них расходуется на "служебные нужны" и максимально доступный объем кучи составляет гигабайт - полтора.
Правда, можно поровну распределить массив coordinate_line
между восемью процессами (ведь возможность читать и писать в "чужое" адресное пространство у нас есть – см. описания функций ReadProcessMemory и WriteProcessMemory в Platform SDK). Конечно, это очень кривое и уродливое решение, но зато крайне производительное. Ну пусть за счет накладных расходов на вызов API-функций алгоритм линейной сортировки превзойдет quick sort не в тысячу, а в шестьсот–девятьсот раз. Все равно он будет обрабатывать данные на несколько порядков быстрее.
Впрочем, ведь далеко не всегда сортируемые данные используют весь диапазон значений _int32: от –2,147,483,648 до 2,147,483,647. А раз так, – потребности в памяти можно существенно сократить! Действительно, количество требуемой памяти составляет: Cmem = N_VAL*sizeof(cell), где N_VAL – кол-во допустимых значений, а sizeof(cell) – размер ячеек, хранящих "зарубки" (они же – дубли). В частности, для сортировки данных диапазона [0; 1.000.000] потребуется не более 4 мегабайт памяти. Это весьма незначительная величина!
Сортировка вещественных типов данных.
До сих пор мы говорили лишь о сортировке целочисленных типов данных, между тем программистам приходится обрабатывать и строки, и числа с плавающей запятой, и...
Первоначально предложенный мной алгоритм действительно поддерживал работу лишь с целыми числами, но после публикации статьи "Немного о линейной сортировке" (ее и сейчас можно найти в сети…) им заинтересовались остальные программисты, среди которых были и те, кто приспособил линейную сортировку под свои нужды.
В частности, линейную сортировку вещественных чисел первым (насколько мне известно) реализовал Дмитрий Коробицын, письмо которого приводится ниже:
----- Original Message -----
From: "Дмитрий
Коробицын" <dvk@nts.ru>
To: "Крис Касперски" <kk@sendmail.ru>
Sent: Friday, June 22, 2001 2:27 AM
Subject: Re: О линейной сортировке
ДК> Сегодня хочу написать про сортировку чисел Float.
ДК> Вы пишете:
КК>> Один только ньюанс - как отсортировать числа по возрастанию? Формат
КК>> float и dooble не сложен, но попробуй-ка вывести все числа в порядке
КК>> возрастания!
Да, действительно для сортировки чисел Float придется построить функцию long int f(float x), такую, чтобы для любых x и y, если x<y, то f(x) < f(y). Не вызывает сомнения, что такую функцию построить можно, но весь вопрос в том, насколько она сложна и сколько шагов потребуется от компьютера для ее реализации? Сразу оговоримся, что трудоемкость этой функции от размера массива чисел не зависит, следовательно это константа, и на трудоемкость всего алгоритма она повлиять не сможет. Он так и останется линейным. Чтобы сильно не злоупотреблять Вашим вниманием, забегая вперед, хочу сразу сказать, что эта функция очень простая. Проще не бывает. Это "функция правды", как Вы назвали ее в одной из своих статей, а именно f(x) = x, то есть преобразовывать ничего не нужно. Нужно просто компилятору сказать, что в этих ячейках лежит не число float, a long int.
Доказательство: Float устроен следующим образом: 32 бита в памяти, самый старший бит это знак, тоже и у четырехбайтового целого числа. После бита знака следующие 8 битов "смещенный порядок" - показатель степени двойки.
Для положительных чисел float, чем больше порядок, тем больше число, но, с другой стороны, для положительного длинного целого чем большее число записано в старших битах, тем число больше. Оставшиеся 23 разряда – это значащая часть числа, мантисса. Значение положительного числа float получается следующим образом:
Значение = (1+мантисса*2^(-23)) * 2 ^ (смещенный порядок -127) Здесь следует пояснить, что если мантисса равна нулю, то значение числа float совпадает со степенью двойки. Если все биты мантиссы установлены в 1 (самая большая мантисса = 0x7FFFFF = 2^23 - 1), то получаем 1 + 0x7FFFFF*2^(-23) = 1.99999988079071044921875
Получаем, что для положительных float при одинаковом значении "смещенного порядка" чем больше мантисса, тем больше число, но для длинного целого та же ситуация, при одинаковых старших битах чем большее значение записано в младших битах тем больше число. Рассмотрим еще ситуацию, когда при увеличении числа меняется "смещенный порядок".
Возьмем для примера числа 1.99999988079071044921875 и 2.0 оба этих числа положительные, значит старший бит равен нулю. У первого показатель степени двойки равен 0 значит "смещенный порядок" = 127 = 0111 1111. Мантисса состоит вся из 1.
Следовательно в памяти это будет выглядеть так - старшие два бита равны 0, остальные - 1. У второго числа показатель степени двойки равен 1, а значение мантиссы равно 0. Смещенный порядок = 128 = 1000 0000. В памяти - все биты кроме второго равны 0.
Шестнадцат. Целое число Float
0x3F FF FF FF 1073741823 1.99999988079071044921875
0x40 00 00 00 1073741824 2.0
Еще несколько чисел:
Шестнадцат. Целое число Float
0x3D CC CC CD 1036831949 0.100000001490116119
0x3E 4C CC CD 1045220557 0.200000002980232239
0x3E 99 99 9A 1050253722 0.300000011920928955
0x3E CC CC CD 1053609165 0.400000005960464478
0x3F 00 00 00 1056964608 0.5
0x3F 19 99 9A 1058642330 0.60000002384185791
0x3F 33 33 33 1060320051 0.699999988079071045
0x3F 4C CC CD 1061997773 0.800000011920928955
0x3F 66 66 66 1063675494 0.89999997615814209
0x3F 80 00 00 1065353216 1.0
0x40 00 00 00 1073741824 2.0
0x40 40 00 00 1077936128 3.0
0x40 80 00 00 1082130432 4.0
0x40 A0 00 00 1084227584 5.0
0x40 C0 00 00 1086324736 6.0
0x40 E0 00 00 1088421888 7.0
0x41 00 00 00 1090519040 8.0
0x41 10 00 00 1091567616 9.0
0x41 20 00 00 1092616192 10.0
Из приведенной таблицы видно, что при возрастании числа float возрастает и соответствующее ему целое число. Заметим, что целое число ноль соответствует нулю с плавающей точкой.
Таким образом, для неотрицательных чисел никакого преобразования не требуется. Как же быть с отрицательными числами?
Отрицательные целые числа хранятся в дополнительном формате,то есть целому числу минус один соответствует 0xFF FF FF FF, а это самое большое по модулю отрицательное число (в действительности компьютер считает, что это "нечисло"). Числу минус десять миллионов соответствует float примерно равный минус три на десять в 38 степени.
Шестнадцат. Целое число Float
0xFF 67 69 80 -10000000 -3.07599454344890991e38
0xFA 0A 1F 00 -100000000 -1.79291430293879854e35
0xC4 65 36 00 -1000000000 -916.84375
0xC0 00 00 00 -1073741824 -2.0
0xBF 80 00 00 -1082130432 -1.0
0xBF 00 00 00 -1090519040 -0.5
0xA6 97 D1 00 -1500000000 -1.05343793584122825e-15
0x88 CA 6C 00 -2000000000 -1.21828234519221877e-33
Из приведенной таблицы видно, что чем больше по модулю отрицательное целое число, тем меньше по модулю число float. Неужели придется проверять знак у числа, и если оно отрицательное, то делать преобразование? На самом деле нехитрым программистским приемом избавляемся от всяких преобразований. Сначала прейдем от целых чисел со знаком к целым числам без знака. При этом преобразования не потребуются, просто область памяти вместо long int надо определить как unsigned long. (Заметим, что на сортировку положительных чисел это никак не повлияет.) Далее заметим, что самому большому по модулю отрицательному числу float вместо минус единицы теперь будет соответствовать 0xFF FF FF FF – это (два в степени 32) - 1.
Таким образом, самое большое целое число без знака будет соответствовать самому большому по модулю отрицательному числу. Но если теперь у нас все целые числа не имеют знака, то как же отделить положительные float от отрицательных? Потребуются преобразования? Нет!
Пример программы:
Программу напишем в виде функции, которой на вход передается не отсортированный массив float и его размер - n. После работы функции массив должен быть отсортирован по возрастанию.
void Sort(float *u, unsigned long N)
{
unsigned long *a,*int_u, c, n, k;
PrepareMem(&a);
// преобразуем указатель. Предполагая, что
sizeof(float) = sizeof(long)
int_u=(unsigned long *)u;
// сортировка
for (c=0; c < N; c++) a[int_u[c]]++;
// формируем отсортированный массив
k=0;
// сначала отрицательные числа, начиная с самых больших по модулю
for(c=0xFFFFFFFF; c > 0x7FFFFFFF; c--)
for(n=0; n < a[c]; n++)int_u[k++]=с;
// теперь положительные числа, начиная с (float) нуля.
for(c=0; c < 0x80000000; c++)
for(n=0; n < a[c]; n++)int_u[k++]=с;
}
Заметим, что инициализация памяти выделена в отдельную функцию. Во-первых, не плохо было бы проверить, чем закончилось выделение 16 гигабайт памяти. Во-вторых, на забивание массива нулями тратится почти половина времени работы алгоритма. Я предполагаю, что используя прямой доступ к памяти (DMA) это время можно сократить.
---- конец письма ---